Dasar dasar untuk semua ajaran yang mengenal dunia adalah matematika. Penggunaan ilmu pasti bahasa formal dan mempelajari urutan, struktur, dan hubungan pada objek abstrak yang dipilih. Tidak semua peserta didik menyukai matematika karena hal itu kompleksitas dan kebingungan, tetapi kemungkinan besar karena kesalahpahaman. Perubahan yang bertahan dalam kaitannya dengan matematika akan membutuhkan dedikasi, konsentrasi, konsistensi, bahkan keras kepala dan, yang paling penting, solusi praktis. Dalam penelitian ini, adalah penting langkah demi langkah untuk memahami awalnya yang sederhana dan secara bertahap beralih ke yang lebih kompleks, tanpa meninggalkan apa pun yang tidak dapat dipahami dan dipahami..
Ada banyak cabang matematika yang berbeda yang telah cukup dipelajari dan muncul baru-baru ini. Berikut ini menjelaskan dasar-dasar analisis matematika - konsep dasar awal, definisi dan aturan untuk mempelajari fungsi-fungsi sederhana dari satu variabel, turunan dan diferensiasi.
Pepatah muncul di antara siswa sekolah dasar: "Matematika menjadi sangat rumit ketika angka hilang dari itu." Memang, mereka datang lebih dekat untuk memahami beberapa definisi dan hukum sains matematika dengan memutuskan aturan menggunakan contoh nyata..
Definisi Kunci
Mari kita mulai dengan terminologi - dengan makna semantik umum sederhana dari definisi utama:
- Variabel - nilai atau simbol, dapat mengambil salah satu dari sejumlah nilai di
area spesifik (berat atau tinggi anak)
- Fungsi - tujuan, pekerjaan, aktivitas, tindakan spesifik pada variabel, kami menunjukkan f (x) (ketergantungan berat anak pada tinggi badannya)
- Batasi - batas, batas, tepi (horizon - bidang tampilan)
- Derivatif - terbentuk, sekunder, mengalir dari yang lain, kami menunjukkan f '(x) (kecepatan saat bergerak)
- Diferensial - perbedaan, perbedaan, pemisahan.
Fungsinya adil
Fungsi adalah hasil dari apa yang dilakukannya dengan variabel, yaitu hasil perhitungan. Ini adalah hubungan elemen di mana perubahan dalam satu variabel menyebabkan perubahan pada variabel lainnya. Bagilah f (x) menjadi sederhana dan kompleks.
Metode berikut digunakan untuk menampilkan dependensi: aljabar, grafik, tabel, logis, dan bahkan perangkat lunak.
Ketergantungan numerik ditentukan secara aljabar menggunakan simbol variabel, persamaan dan ketidaksetaraan (≤ dan>), persamaan bentuk dibangun: y = f (x), di sini x adalah variabel atau argumen, dan y atau f (x) adalah fungsi. Untuk setiap nilai spesifik dari variabel x dari domain definisi yang dapat diterima, ada yang sesuai dengan nilai y untuk f (x).
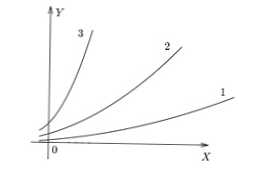
Gambar di bawah ini menunjukkan grafik sederhana dari 3 rasio yang berbeda. Dapat dilihat bahwa dalam f (x) 3 nilai y terbesar diperoleh untuk x spesifik, dalam f (x) 1 - terkecil.
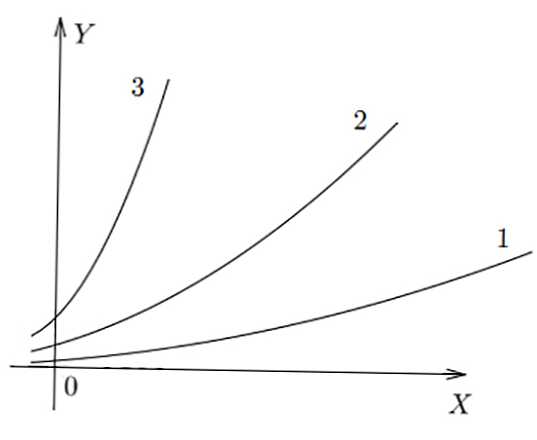
Fungsi
Ekspresi dasar berikut dibedakan: linear (langsung), kuadratik (parabola), kubik, hiperbola, eksponensial, logaritmik, trigonometri (ditunjukkan pada tabel di bawah).
Untuk analisis masing-masing jenis f (x), sifat-sifat inherennya ditentukan (dicantumkan di bawah ini); untuk ini, konsep derivatif dan diferensial digunakan.
Fungsi turunan
Derivatif - operator, yang untuk f (x) asli sesuai dengan hukum diferensiasi mengaitkan fungsi lain, itu mencirikan perubahan dalam f (x) utama dari argumen x di beberapa titik. Untuk pemahaman terperinci tentang hal itu, seseorang harus berurusan dengan definisi yang lebih kompleks tentang batas ketergantungan dan diferensiasi..
Batasi - definisi ini dinamis. Ekspresi yang x cenderung n dipahami sebagai berikut: x memperoleh nilai yang dekat dengan n dan berbeda dengan jumlah kecil.
Diferensial - perubahan kecil besarnya. Peningkatan ini disebut delta.
Derivatif untuk f (x) pada suatu titik adalah batas untuk membagi delta fungsi dengan delta variabel pada titik tertentu, jika yang terakhir cenderung ke 0.
Karakteristik laju perubahan ketergantungan pada titik tertentu, secara geometris dapat ditunjukkan sebagai nilai tan dari sudut kemiringan alpha tangent terhadap fungsi.
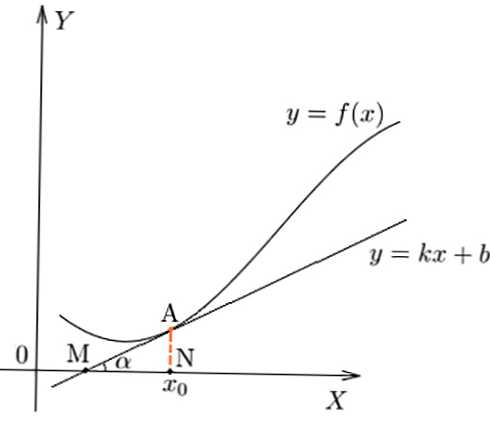
Derivatif
Ketergantungan disebut dapat dibedakan jika f '(x) didefinisikan. Menemukan turunan disebut diferensiasi. Aturan untuk menghitung f '(x) dan mencocokkan f' (x) dari SD f (x) diberikan dalam tabel di bawah ini
Fungsi yang diturunkan juga berfungsi
Setiap ketergantungan memiliki sifat tertentu, mengetahui dan mengeksplorasi mereka Anda dapat menganalisis sifat negara dan mengubah f (x).
Sifat utama:
- Definisi dan Nilai Kesenjangan Data.
- Nol f (x)
- Fungsi bertambah atau berkurang dalam beberapa interval.
- Poin MAX dan fungsi MIN, apakah ada belok.
- Genap atau ganjil f (x)
- Fungsi terbatas dan tidak terbatas.
- Apakah ada asimtot?.
- Frekuensi f (x).

Fungsi dan Derivatif
Ketika menetapkan karakteristik ketergantungan menggunakan turunan, interkoneksi properti f '(x) dengan properti f (x) dan sebaliknya digunakan. Karakteristik f '(x) mudah ditentukan pada grafik fungsi, dan sebaliknya, karakteristik f (x) primer dipahami dari grafik f' (x). Memperbaiki esensi dari setiap fitur fungsi, menyelidiki dan membangun rantai hubungan. Untuk menentukan asimtot dalam grafik, konsep batas digunakan..
Berikut adalah beberapa karakteristik dan ketergantungan f '(x) pada f (x):
- Ketika f (x) meningkat dalam interval, f '(x) positif.
- Jika f (x) menurun selama interval, f '(x) negatif.
- Di hadapan f (x) titik MAX, f '(x) = 0 di dalamnya mungkin tidak ditentukan, dan tg dari sudut singgung mengubah tanda dari + ke -.
- Di hadapan f (x) titik MIN, f '(x) = 0 di dalamnya mungkin tidak ditentukan, dan tg dari sudut tanda tangen berubah dari - ke +.
- Ketika menekuk f (x) dalam E, nilai f '(x) tidak mengubah tanda pada titik, f' (x) = 0.
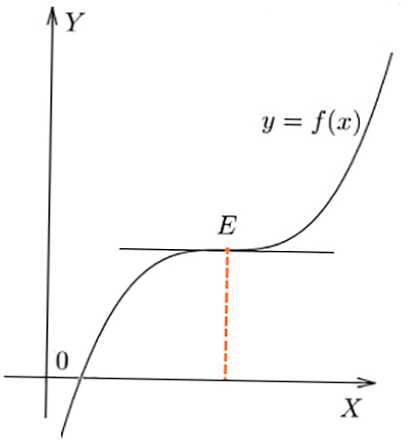
Infleksi pada titik E dari grafik fungsi
Untuk penelitian, f (x) membuat skema di mana setiap langkah dibangun sesuai dengan algoritma spesifik untuk menghitung dan menganalisis hubungan elemen komponen.
Perbedaan Fungsi dan Derivatif
Aturan penjumlahan dan pengurangan f (x) sama dengan aturan tindakan ini selama diferensiasi. Tetapi aturan untuk menemukan f '(x) di bawah tindakan perkalian dan pembagian fungsi berbeda (seperti dalam tabel).
Fungsi ini primer, dan turunannya adalah operasi matematika sekunder, dalam kebanyakan kasus mereka memiliki karakteristik yang berbeda.
Titik belok ketergantungan terus-menerus ditemukan oleh turunan keduanya, tandanya harus berubah di wilayah titik x0.
Ada beberapa jenis fungsi yang tidak memiliki f '(x) pada titik x0 (terputus-putus). Dalam ekspresi ln (| x | -1) turunannya tidak didefinisikan pada titik x0 = 1.
Ada ungkapan "modulo" mirip dengan y = | x |, yang memiliki ketegaran di x0.
Untuk dependensi seperti itu, hanya sebagian (pada interval domain definisi) yang digunakan untuk mempelajari sifat-sifatnya menggunakan derivatif dan tidak selalu mungkin untuk beralih dari properti f '(x) ke properti primer.
Tidak ada yang bisa dilakukan tanpa kecuali aturan, dan bahkan dalam matematika. Untuk mengurai dan mengkonsolidasikan materi yang disajikan, sangat penting untuk menyelesaikan contoh, praktik, mendapatkan pengalaman dengan batasan, perbedaan dan turunannya, dan dengan berani beralih ke integral.











